Как нарисовать куб карандашом объёмно

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями.

Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть.

Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать.

Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Поделки из бумаги – увлечение на всю жизнь

Что-то делать руками всегда интересно и полезно, особенно если получается красиво. Ручная несложная работа помогает успокоить нервы после тяжелого трудового дня и развивает фантазию (особенно у детей). В Китае данный вид творчества известен как оригами, и давно с успехом помогает лечить душевнобольных людей и детишек, страдающими нервными заболеваниями. Такие занятия повсеместно применяются на уроках труда в школах или в старших группах в детских садах, что позволяет развить усидчивость, воображение и мелкую моторику, которая в свою очередь развивает умственную деятельность. Часто детские журналы предлагают схемы различных зверюшек, фигурок для совместной работы взрослых с детьми. Мы предлагаем схемы кубиков из бумаги или картона с различными вариантами картинок. Такие поделки будут интересны как малышам, так и школьникам, их можно преподнести в качестве подарка, сделанного своими руками. Взрослые так же могут использовать сделанные по нашим разверткам кубики, например кубик-календарь.

Пошаговая инструкция: как сделать куб из картона

1. Распечатайте необходимое количество шаблонов, например для кубика-календаря – необходимо оба варианта, а для кубиков с алфавитом – распечатайте столько, сколько нужно для складывания слов. 2. Аккуратно вырежьте схему куба. Вырезать удобнее ножницами, но можно воспользоваться и канцелярским ножом. 3. Согните вырезанный шаблон куба по линиям, чем аккуратнее вы согнёте схему куба, тем лучше будет смотреться ваше изделие. 4. Смажьте затемненные участки клеем и сторону за стороной соберите весь куб.

Развертка простого куба (грань 5 см)	Развертка куба с арабскими цифрами 1,2,3,4,5,6 (грань — 5 см)	Развертка куба с арабскими цифрами 7,8,9,0,1,2 (грань — 5 см)

Развертка куба с римскими цифрами I, X, L, C, V, D (грань — 5 см)	Развертка куба с римскими цифрами I, M, V, X, ↁ, ↂ (грань — 5 см)	Куб с формулами (грань — 5 см)

Схема куба с английским алфавитом A, B, C, D, E, F (грань 6,5 см)	Схема куба с английским алфавитом G, H, I, J, K, L (грань 6,5 см)	Схема куба с английским алфавитом M, N, O, P, R, Q (грань 6,5 см)

Схема куба с английским алфавитом S, T, U, R, V, W (грань 6,5 см)	Схема куба с английским алфавитом X, Y, Z, A, B, C (грань 6,5 см)	Схема куба с русским алфавитом А, Б, В, Г, Д, Е (грань 6,5 см)

Схема куба с русским алфавитом Ж, З, И, Й, К, Л (грань 6,5 см)	Схема куба с русским алфавитом М, Н, О, П, Р, С (грань 6,5 см)	Схема куба с русским алфавитом У, Ф, Х, Ц, Ч, Т (грань 6,5 см)

Схема куба с русским алфавитом Ш, Э, Ъ, Ы, Ь, Щ (грань 6,5 см)	Схема куба с русским алфавитом Ю, Я, А, Б, В, Г (грань 6,5 см)	Схема куба с материками (грань 6,5 см)

Схема куба с портретами ученых

И еще немного о кубиках из бумаги

Сейчас детские магазины переполнены всякими игрушками, в том числе и развивающими. Можно найти практически всё на любой возраст и кошелёк. Но иногда бывет трудно найти кубики, которые нам знакомы с детства. Кубики – это своего рода конструкторы, с которыми с удовольствием играют детишки. По рекомендациям педагогов, психологов и педиаторов малышам до 1 года уже можно давать игрушки-кубики. Они отлично развивают не только координацию, воображение, но при этом задействуют практически все мышцы рук, что прекрасно развивает мелкую моторику малыша. Из какого только материала не делают кубики – и из пластика, из дерева, из стекла, мы предлагаем вам сделать кубики из бумаги. Кубики с картинками с изображением цифр или букв будут прекрастным подспорьем для родителей и воспитателей в процессе подготовки ребёнка к школе. Более того, игра с кубиком даст малышу представление о геометрическх фигурах, в частности о кубе, о его свойствах. Если вы распечатаете и другие объемные геометрические фигуры (пирамиды, тетраэдр и т.д.), это значительно расширит кругозор ребёнка и поможет в процессе обучения в школе. Совместные занятия взрослых и детей очень сближают и укрепляют семью.

Сейчас практически в каждом доме есть компьютер и принтер, т.е. ваши затраты – это стоимость бумаги, формата А4. Приведённые на данной странице шаблоны куба можно редактировать, т.е. взяв чистую развёртку куба, вы можете смело вставлять свои картинки и распечатать новый вариант. В качестве картинок можно взять рисунки или фотографии зверей, животных, машин, а так же фотографии знаменитостей или своих родственников, полет фантазии безграничен. Успехов вам в творчестве и в воспитании!

Развертка и схема куба из бумаги

Разноцветный куб 1 (грань 6,5 см)	Разноцветный куб 2 (грань 6,5 см)	Игральный куб (грань 5 см)

Куб-календарь на 2013 год (январь-июнь, грань 6,5 см)	Куб-календарь на 2013 год (июль-декабрь,грань 6,5 см)

Григорий Андреев

Гиперкуб в искусстве

Гиперкуб появился в научно-фантастической
литературе с 1940 года, когда Роберт Хайнлайн
в рассказе «Дом, который построил Тил» («And He Built a
Crooked House») описал дом, построенный по форме
развертки тессеракта. В рассказе этот Далее
этот дом сворачивается, превращаясь в
четырехмерный тессеракт. После этого
гиперкуб появляется во многих книгах и
новеллах.

В фильме «Куб 2: Гиперкуб»
рассказывается о восьми людях, запертых в
сети гиперкубов.

На картине Сальвадора Дали «Распятие»
(«Crucifixion (Corpus Hypercubus)», 1954) изображен
Иисус распятый на развертке тессеракта. Эту
картину можно увидеть в Музее Искусств (Metropolitan Museum of
Art) в Нью-Йорке.

Кубик техникой оригами

Существует огромное количество способов сборки фигур в технике оригами. Но для простоты следует изучить самый простой метод, для которого требуется осуществить следующие действия:

1Приготовить форму – стандартный квадрат из бумаги. Картон лучше не использовать, поскольку он плотный и собрать из него фигуру будет неудобно.

2Сложить квадрат пополам вдоль одной стороны и по диагонали в каждом направлении. Складывают лист по стороне и по диагоналям в противоположные направления: по стороне в одном направлении, по диагоналям в противоположные. Сделать треугольник, как представлено на картинке.

Схема сборки куба в технике оригами

3Одну часть треугольника отделить, приставить ее к середине и загнуть – получится, что угол поднимется к вершине треугольной основы. Аналогичным образом делают со второй стороной.

4Далее у уменьшенных треугольников углы, расположенные в разные стороны, направляют друг к другу – сгибают вершину треугольника пополам.

5Затем требуется согнуть свободную вершину треугольника в более меньший. Продолжить сгиб так, чтобы собранная вершина смогла разместиться между двумя прослойками предварительной треугольной заготовки.

6Расположить будущую фигуру на столе и загнуть оставшиеся треугольные верхушки вовнутрь. Получится, что загнуться две верхушки – их необходимо только загнуть и разогнуть обратно. Эти действия только формируют грани будущего куба. Аналогичным образом делают грани будущей фигуры, согнув вершины в противоположную сторону и также расправив их.

7Далее расправляют основу, отправив вовнутрь стороны с согнутыми треугольниками.

8В одной вершине треугольника сформировалось отверстие, в которое задувают, чтобы расправить заготовку для формирования куба.  .

Получился стандартный куб с одинаковыми гранями и равными сторонами. Его можно использовать для декора и прочих действий. Написать на нем что-то будет сложно, но возможно. Поскольку изделие получается большим, их рекомендуется использовать для игр с маленькими детьми – с малышами и дошкольного возраста.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями.

Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть.

Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать.

Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Построение куба в перспективе

При построении куба нужно исходить из того, что все его стороны и грани равны. Однако, с визуальной точки зрения все грани куба будут равны только в случае, если он расположен точно перед смотрящим, а обращенная к смотрящему сторона куба точно перпендикулярна его взгляду. Во всех остальных случаях будут иметь место перспективные сокращения.

Учитывая одинаковость всех сторон куба очень важно правильно измерить визуальное направление линий граней куба, их размеры и положение относительно друг друга. Если при замерах будут неточности, которые перекочуют в рисунок, в дальнейшем, при восприятии готового изображения, зритель невольно будет ощущать, что куб имеет не совсем правильные формы

Если куб расположен прямо перед зрителем

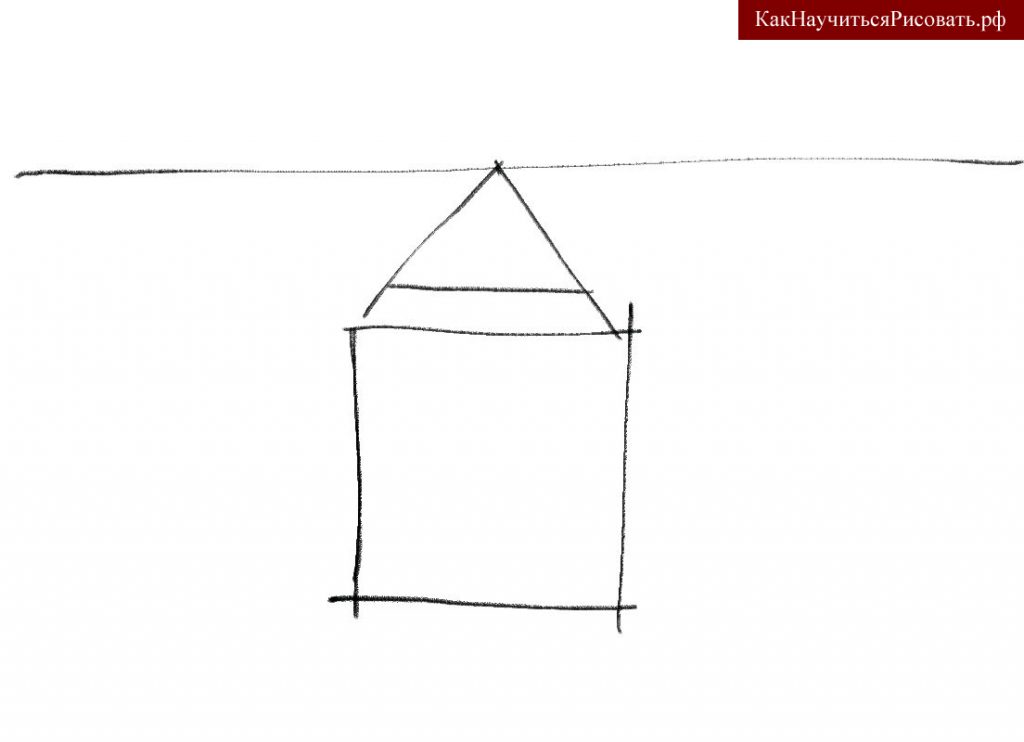
Здесь рассмотрим только вариант расположения куба прямо перед зрителем ниже линии горизонта. В этом случае будут видны две стороны куба: фронтальная и верхняя. При учебном рисовании фронтальную сторону можно изобразить в виде обычного квадрата.

Для построения верхней стороны куба требуется нарисовать линию горизонта. Затем на линии горизонта отметить , которая будет расположена точно посередине ранее нарисованного квадрата. Далее следует соединить два верхних угла квадрата с точкой схода. При рисовании с натуры на следующем этапе нужно измерить соотношение высоты видимой фронтальной стороны куба и видимой верхней стороны. Далее это соотношение перенести на рисунок и отметить дальнюю грань верхней стороны куба. После этого провести горизонталь через полученную отметку до линий, уходящих к точке схода. Если рисуется воображаемый куб, то последние описанные выше действия придется делать на глазок, как подсказывает интуиция.

Если куб расположен под углом к зрителю

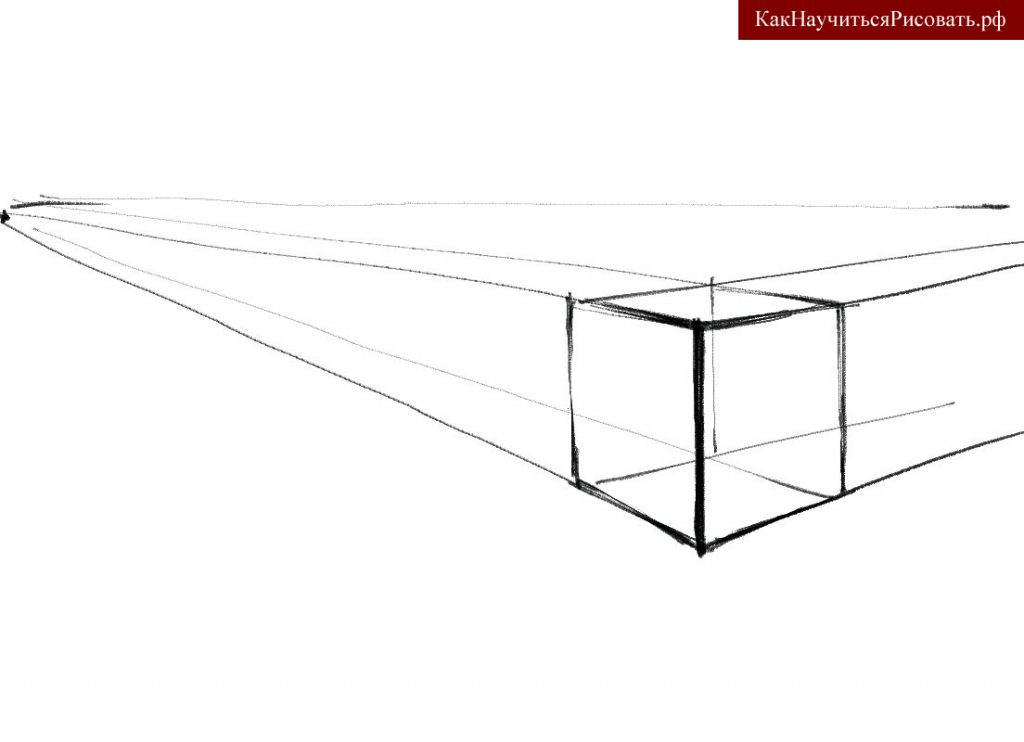
При расположении куба отличном от точно фронтального, будут видны две или три стороны куба и при построении на линии горизонта образуются . Рассмотрим случай, когда куб расположен ниже линии горизонта под углом к смотрящему. При таком положении куба будут видны три его стороны.

Для начала нужно нарисовать вертикальную линию, которая будет обозначать ближайшую к зрителю грань куба. После этого требуется определить нахождение линии горизонта относительно нарисованной вертикали и отобразить ее. Затем нужно измерить направление исходящих от ближайшей вертикальной грани тех граней, которые сопряжены с ней и уходят в перспективу. После чего следует мысленно перенести направления перспективных граней на рисунок и провести по ним линии от ближайшей вертикальной грани до пересечения их с линией горизонта. Если сделать все правильно, то все грани, уходящие влево от указанной вертикали сойдутся в одной точке схода слева. Те же грани, что визуально уходят вправо сойдутся во второй точке схода на линии горизонта, расположенной справа от первой вертикали.

После этого нужно измерить видимую ширину вертикальных правой и левой сторон куба. На основании замеров провести вертикали, обозначающие дальние вертикальные грани куба. При этом вертикали пересекутся с гранями, уходящими в перспективу. От точек их пересечения с верхними перспективными гранями следует провести линии, уходящие к точкам схода в следующей последовательности: от левой грани к правой точке схода, от правой грани к левой точке схода. При пересечении последних проведенных линий образовался самый дальний от зрителя угол куба.

Из самого дальнего верхнего угла куба проводим вертикаль вниз. Из самого левого нижнего угла проводим линию в точку схода справа, из правого угла в левую точку схода. Последние две линии в идеале должны пересечься между собой в том же месте, где они пересекаются с последней проведенной вниз вертикалью. В этом абзаце описано построение невидимых граней куба. Они дают понимание устройства куба, что пригодится при дальнейшем рисовании.

Очень важное замечание! Часто при построении более одной точки схода они могут располагаться за пределами рисунка. В этом случае их можно дорисовывать на поверхности, на которой расположен лист с рисунком

Либо мысленно достраивать, запоминая их расположение в пространстве для дальнейших построений.

Объемные бумажные кубики без клея и ножниц

Задумывались ли вы о том, как сделать куб из бумаги и зачем это нужно? Допустим, как сделать кубик из картона своими силами, мы вам расскажем и даже покажем.

А какими полезными функциями вы наделите кубик оригами? Подскажем: вспомните свои детские кубики с буквами, из которых вы учились складывать первые слова, еще не умея писать.

А если бумажный кубик оклеить картинками из старых детских книжек, получится не менее интересный, чем в нашем далеком детстве, пазл-конструктор.

Вариантов игрового применения куба из цветной бумаги не счесть. И при этом не придется переживать, что дети поранят друг друга, кидая такую игрушку. Наши-то деревянные были потяжелее. Мы уже готовы показать, как сделать кубик из бумаги своими руками прямо сейчас. Готовы приступать?

Простой бумажный кубик

Объемный шестигранный куб 3Д складывают из квадратного листка бумаги без клея. И даже ножницы здесь не потребуются. Разве что отрезать лишний «хвостик» от листа А4, чтобы получить заготовку-квадрат. Зато пригодится навык надувания воздушных шариков, ведь мы сейчас научим вас тому, как сделать надувной кубик. Заинтригованы? Тогда начнем:

• Схема 1 — ваш наглядный ориентир. К нему следует прибегать каждый раз, когда алгоритм складывания кажется сложным. Возьмите бумажный квадрат и сложите его по диагоналям, затем пополам — все это просто разметка;
• Ориентируясь на диагонали-сгибы, сформируйте треугольник, подгибая внутрь боковые плоскости заготовки (см. схему). 4 гуляющих угла у основания треугольника нужно подогнуть к вершине по 2 с каждой стороны заготовки;
• Боковые противоположные уголки подогните к центру — у вас здесь есть вертикальная ось-ориентир. Повторите действие с другой стороны. Гуляющие уголки одного из конических выступов (на втором углы «закрыты») дважды подгибают, чтобы их можно было аккуратно заправить в срединные уголки-кармашки;
• Аналогично заправьте дважды сложенные уголки в кармашки с обратной стороны заготовки. Модель куба готова, осталось дать ей объем. Найдите открытый уголок и через него надуйте макет.

Куб из модулей: сборный кубик 6 цветов

Как сделать кубик из картона своими силами мы уже рассмотрели выше, а для этого модульного куба будет достаточно разноцветной бумаги 6-ти расцветок (или 3-х повторяющихся). Он и без картона получится достаточно плотным за счет алгоритма складывания модулей (каждого в отдельности и всех воедино).

Давайте начнем разбираться поэтапно. Сразу предупредим, что весь процесс будет разделен на 7 шагов — складывание модулей и сборка куба (можно на клей — будет прочнее).

Какое-то время будет потрачено, но результат вас однозначно порадует: кубики получатся яркими, разноцветными, не нуждающимися в дополнительных украшениях или росписи.

• Возьмите квадратный листок бумаги и сложите его так, чтобы получилось видимое разделение на 4 одинаковых прямоугольных плоскости (см. рис. 2). Загните малые уголки по диагональным углам стартового квадрата;
• Заверните «створки» листа подобно закрытию оконных ставней. Используя ориентиры-уголки (подогнутые ранее), загните внутрь незадействованные прежде углы, потом заправите их внутрь с обеих сторон. Получится параллелограмм;
• Переверните конструкцию вниз лицом, отогните уголки к себе так, чтобы получился маленький квадрат с треугольными ушками-отгибами. Сделайте еще 5 шт. таких модулей.

Соединяйте блоки в куб, вводя уголки модулей в срединные плоскости-кармашки соседних блоков. Проявите смекалку, в крайнем случае поможет схема. Как сделать оригами кубик из ярких модулей, вы освоили на практике. Попробуйте склеить куб из блоков на этапе сборки, чтобы он был еще прочнее и не рассыпался на модули в игре.

Можно, конечно, взять стандартную развертку куба, просто распечатать ее и склеить — готовые шаблоны всегда под рукой. А если типовая выкройка вас не устраивает и в игру нужен оригинальный счетный кубик, вы на раз-два сможете его сложить сами. Чего проще, когда знаешь, как сделать из бумаги еще и не такие премудрости.

Возможно, вас заинтересуют схемы складывания бумажной гадалки или лягушки, которая открывает рот.

О внешнем виде всех 3ПГК-n

Вот аналогия: все 3ПГК-n как на их чертежах, так и в самих моделях, своей внешней
геометрической формой напоминают «юлу» (или волчок). И чем выше измерение,
тем все более и более 3ПГК-n напоминает форму «юлы».

В идеально построенных чертежах 3ПГК-n, где n≥5, существует только одна горизонтальная
проекция 3ПГК-n, фронтальных и профильных проекций – сколь угодно много, а проекций в
ракурсах под определенным углом зрения – бесчисленное множество.

Итак, чтобы построить горизонтальную проекцию 3ПГК-n, надо сначала построить горизонтальную
проекцию ее «исходной» правильной n-угольной пирамиды, то есть построить правильный n-угольник. – Всего-то!

Еще раз обращаю ваше внимание на факт, что на тетрадном листе бумаги «в клетку»
через вершины квадратных «клеток», кроме самого квадрата, невозможно построить
все остальные правильные многоугольники (треугольник, пятиугольник,
шестиугольник, …, десятиугольник, …, и т.д.).

Автор каждое ребро многоугольника в моих чертежах рассматривает как гипотенузу и
проверяет ее теоремой Пифагора. Пытаясь построить эти правильные многоугольники
«по вершинам «клеток»», он добивается наименьшей погрешности в чертежах.

Я каждое ребро многоугольника в моих чертежах рассматриваю как
гипотенузу и проверяю ее теоремой Пифагора. Пытаясь построить эти
правильные многоугольники «по вершинам «клеток»», я добиваюсь
наименьшей погрешности в чертежах.

Казалось бы, черчение 3ПГК-n «по вершинам клеток» — недостаток.
Но этот «недостаток» можно превратить в «достоинство» данного способа
построения проекций 3ПГК-n, особенно при построении горизонтальных проекций 3ПГК-n.
Как уже упоминалось ранее, не рекомендуется начинать построение горизонтальных проекций 3ПГК-n,
пользуясь идеально правильной проекцией «исходной» правильной n-угольной пирамиды, —
у вас будет на чертежах (особенно при n = четному числу) совмещение вершин, ребер,
граней и даже кубов. Это нормально, правильно. Чаще всего это – визуальное совмещение.

Матрица перемещения

Матрица перемещения воздействует на точку, но вектор сохраняет неизменным. Действует она так:

В GLM есть функция , умножающая переданную матрицу на матрицу перемещения. Чтобы анимировать куб, будем вычислять смещение по оси Ox в каждый момент времени. После этого получение матрицы перемещения будет очень простым:

Для гладкого движения куба будем использовать прямолинейное равномерно ускоренное движение, аналогичное обычному прыжку или движению мача, брошенного вверх. Вот его иллюстрация в неинерциальной и инерциальной системах отсчёта:

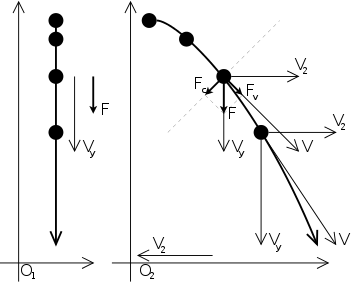
В процессе анимации от 0% до 100% куб должен один или несколько раз прыгнуть в сторону и затем вернуться обратно. Для этого воспользуемся делением с остатком, а также формулой расчёта расстояния на основе начальной скорости и противоположно направленного ускорения. Можно написать так:

Накладывание линий на куб

Техники штриховки и правила ее наложения были описаны не случайно, они на прямую влияют на штриховку карандашом геометрических фигур, в частности куба. Зная эту информацию, не должно возникнуть никаких проблем на практике.
В первую очередь следует нарисовать куб и выбрать какую технику использовать. На примере выбрана перекрестная штриховка.

На переднем плане рисуются прямые параллельные вертикальные линии, а с боку горизонтальные.

Параллельными линиями под наклоном штрихуем куб, перекрывая первый слой линий, как спереди, так и сзади.

Готово!

Таким же незамысловатым способом можно наложить другие типы линий и использовать другие техники.

Однако этот способ простой, он подойдет для новичков, чтобы просто научиться штриховать. Если вами уже пройден этот этап, берите рисунок куба, учитываете его положение, падающие свет и тень и старайтесь перенести увиденное на бумагу. При этом вами будут использованы те же техники, просто нужно будет поиграть с количеством линий, их плотностью и толщиной. Таким образом вы передадите самые темные и светлые места фигуры и сделаете ее объемной.

Как видите, ничего сложного и сверхъестественного делать не нужно. Практикуйтесь и результат не заставит себя долго ждать. Рисуйте сразу несколько кубов и штрихуйте разными способами. Такое упражнение поможет вам определить, какая техника получается лучше всего и качественнее. Если сложно на первоначальном этапе рисовать куб, тренируйтесь на листке в клеточку, а потом рисуйте от руки. Или накладывайте штрихи на квадрат, но так не получится научиться затенять фигуру.
Практикуйтесь, следуйте правилам и экспериментируйте, может быть вы придумаете, как по-своему заштриховать объект, чтобы получилось красиво. Рисование не точная наука, можно творить по велению сердца.

Базовая терминология

Для того, чтобы мы приступили к изучению рисунка куба карандашом, нам стоит разобрать терминологию, которую мы будем использовать:

Линия горизонта — базовое понятие, которое обозначает воображаемую линию, что находится на уровне взгляда художника. Предмет может находится выше, ниже, частично выше и частично ниже линии горизонта. С линией горизонта может совпадать исключительно линейное изображение — бельевая веревка.

Точка схода — воображаемая точка, которая является местом схода всех параллельных линий изображаемого предмета. Точка схода всегда находится на линии горизонта

Правило, которое важно помнить: если все линии на вашем изображении перпендикулярны линии горизонта, то точка входа будет находится перед нами

Воздушная перспектива — вид перспектив, при котором работает следующее правило: чем дальше предмет, тем менее четкие его границы.

Световая перспектива — вид перспектив, при котором работает следующее правило: чем ближе предмет, тем насыщенней его цвета и четче светотени.

Данные знания являются базовыми, и помогут нарисовать первый объемный предмет.

Простой бумажный кубик

Для работы потребуется лист формата А4. Также нужно подготовить ножницы. Чтобы сделать несложное бумажное изделие, необходимо:

1. Альбомный лист сложить напополам по диагонали. Тот кусок, который будет торчать, необходимо отрезать.
2. Развернуть изделие, по итогу получится квадрат.
3. По получившимся линиям изгиба необходимо сложить бумагу, чтобы она стала треугольной формы.
4. Подогнуть левый и правый край к середине детали.
5. Те же самые действия повторить со всех сторон треугольника.
6. К середине загнуть боковые углы.
7. Аккуратно засунуть их в получившиеся кармашки.
8. Те же действия проделать с другой стороны изделия.

Однородное представление точек и векторов.

Давайте будем считать, что трёхмерная точка хранится как четырёхкомпонентный вектор . А вектор хранится как . Всего лишь одно флаговое значение в конце позволяет избежать любых ветвлений в алгоритмах трансформации векторов и точек. Это происходит благодаря свойствам алгебры матриц.

Как известно, можно умножить матрицу на матрицу при условии, что ширина одной матрицы равна высоте другой (иначе операция просто недопустима). Для получения элемента с позицией i,j в новой матрице достаточно взять i-ю строку левой матрицы и j-й столбец правой матрицы. Вот пример:

Как ни странно, умножение 4-х компонентного вектора на матрицу 4×4 тоже возможно! Для этого достаточно считать 4-х компонентный вектор матрицей 4×1. После умножения получится новый 4-х компонентный вектор.

Ещё более удивительно, что любую комбинацию трёхмерных перемещений, поворотов, вращений (и не только их!) можно представить как всего лишь одну матрицу 4×4, называемую матрицей трёхмерной трансформации. При этом умножение матрицы на трёхмерную точки или вектор, записанный в однородном представлении, даёт новую точку или вектор именно так, как этого требуют правила преобразования точек и векторов. Никаких ветвлений, и никакой магии!

Что такое кубический метр (кубометр)

Кубический метр – термин, который получил название от слов куб и метр. Для указания куба применяется специальный символ «³». В большинстве случаев он используется для определения объема. Куб считается фигурой трехмерного пространства, то есть он характеризуется тремя основными показателями: длиной, шириной и высотой. Поэтому стандартный кубометр –это небольшой кубик.

Один кубический метр равен 1000 литров. Высота, ширина и длина составляют по одному метру, в результате чего получается фигура для вычисления объема. Термин использовался для создания распространенного показателя Еврокуб, который сегодня активно применяется в промышленности при перевозке сыпучих и других грузов.

Подобное понятие получило широкое распространение. Его часто используют на рынке строительных материалов или в других случаях, к примеру, в квитанциях на оплату коммунальных платежей.

Пошаговая инструкция по рисованию невозможного куба

1. Начните рисовать три прямые, вертикальные линии. Линии должны быть одинаковой длины, но средняя линия должна располагаться ниже, чем остальные. Затем соедините линии внизу, используя прямые линии. Это формирует боковые и нижние края куба.

2. Нарисуйте четырехугольник или четырехстороннюю форму в верхней части куба.

3. Далее подробно опишите верхнюю панель куба. Нарисуйте меньший квадрат в верхней части куба. Протяните короткую прямую линию от самого верхнего угла этого квадрата. Затем нарисуйте две прямые линии, идущие от этой линии, параллельно сторонам квадрата.

4. Нарисуйте квадрат внутри одной из боковых панелей куба.

ДРУГИЕ ЛЕГКИЕ РУКОВОДСТВА ПО ЧЕРТЕЖАМ:

5. Нарисуйте квадрат в оставшейся боковой панели куба.

6. Нарисуйте короткие прямые линии, идущие от противоположных углов квадратов. Затем нарисуйте две прямые линии, идущие от каждой из коротких линий. Эти линии должны быть параллельны сторонам квадрата.

7. Вытяните три прямые линии из нижнего левого угла куба. Затем вытяните три прямые линии из нижнего правого угла куба. Позвольте нижней и средней линии встретиться. Затем соедините концы линий, образуя прямоугольники.

8. Сотрите направляющие линии из фигур, нарисованных на предыдущем шаге

ДРУГИЕ ЛЕГКИЕ РУКОВОДСТВА ПО ЧЕРТЕЖАМ:

9. Нарисуйте последнюю сторону невозможного куба. Нарисуйте три прямые, параллельные линии, соединяющие верхний и нижний задние углы куба.

10. Раскрась свой невозможный куб.

Ознакомьтесь с нашими руководствами по рисованию искусственных объектов для получения дополнительной информации

определение таблиц фактов и измерений

В мастере кубов на странице Определение таблиц фактов и измерений выберите таблицы фактов и измерений, которые потребуются при создании куба. Если выбран параметр Автоматическое построение для создания куба, то таблицы фактов и измерений, определяемые мастером, выбираются при первом открытии этой страницы. Если мастер определил, что таблица является одновременно таблицей фактов и измерений, то будут выбраны оба столбца. Если мастер определил, что таблица не является ни таблицей фактов, ни таблицей измерений, то не будет выбран ни один из столбцов. Если для конструирования куба таблица не требуется, сбросьте флажки Факт и Измерение .

Если флажок Автоматическое построение не выбран, то необходимые параметры нужно будет выбрать вручную. Это можно сделать на вкладке Таблицы или Диаграмма .

• На вкладке Таблицы приведен список таблиц в формате таблицы. Установите флажок в столбце Факт или Диаграмма .

• На вкладке Диаграмма отображается схема представления источников данных. Таблицы фактов или измерений различаются по цвету. Щелкните в схеме любую таблицу, а затем Факт или Измерение , чтобы установить или очистить выбор соответствующей таблицы. С помощью кнопки Масштаб выберите нужный масштаб.

Примечание

На вкладке Диаграмма можно увеличить или развернуть окно мастера, чтобы просмотреть схему.

Если в представлении источника данных находится таблица измерения времени, выберите ее в списке Таблица измерения времени . Если нет, оставьте <None> выбранным. Это элемент по умолчанию в списке. При выборе таблицы в качестве таблицы измерения времени она также выбирается как таблица измерений на вкладках Таблицы и Диаграмма .

Заключение

Гиперкуб — одна из простейших
четырехмерных объектов, на примере
которого можно увидеть всю сложность и
необычность четвертого измерения. И то, что
выглядит невозможным в трех измерениях,
возможно в четырех, например, невозможные
фигур. Так, например, бруски невозможного
треугольника в четырех измерениях будут
соединены под прямыми углами. И эта фигура
будет выглядеть так со всех точек обзора, и
не будет искажаться в отличие от реализаций
невозможного треугольника в трехмерном
пространстве (см. «Невозможные
фигуры в реальном мире»).

Статья составлена по материалам
Wikipedia